Building a Digit Classifier with a Neural Network
Introduction: Why, What, How
I built this project and blog to provide a simple explanation of how a machine learning model works, focusing on the process behind training it and the challenges I faced during this experiment.
The main idea is that I trained a machine to distinguish between “handwritten” digits (0, 1, 2, 3, 4, etc. you know the digits). You’ll be able to test the model by drawing your own digit and visualize how the whole process works—from drawing to prediction.
My goal is to explain the core concepts that make this work and provide intuition behind some Machine Learning (ML) principles. No prior knowledge is required to follow along, though some background in Linear Algebra and basic programming will help.
The Demo
On the canvas below, you can draw a digit and hit “Predict” to see what number the model thinks you drew. To maximize the accuracy of the prediction, try to draw a clear digit, as best centered as you can.
How Does This Work?
One of the most common types of machine learning models is a Classifier. As the name suggests, classifiers classify data into predefined classes. In our case, the input is a drawing of a digit, and the output is the predicted number.
But how does the machine learn to distinguish a 9 from a 4? The answer is data—a lot of data. By "data," I mean images of handwritten digits, each labeled with its correct value. This is what we call a labeled dataset.
Let’s imagine you’re trying to teach a child to recognize digits. One way you could teach them is by showing them images of each number, tell them which one is which, and then test their understanding. If the child is correct, you reinforce their behavior. If they make a mistake, you correct them. Over time, they learn to recognize the digits more accurately.
In machine learning, this concept is similar. Although we don’t fully understand how the human brain learns, in a machine learning model, everything is governed by math. Despite the different mechanisms, the core idea—learning from examples—remains the same.
Deep Neural Network Implementation
For this project, I built a classifier model, which refers to the task the model performs—classifying digits. But it’s important to clarify that classifiers aren’t a specific type of machine learning model but a description of the task they accomplish.
Let’s take a step back. Classifiers, like the one in this project, belong to a category of algorithms called Supervised Learning algorithms. These algorithms are trained using labeled data, learning to map inputs to correct outputs.
There are other types of learning, like Unsupervised Learning, where the data is unlabeled. In this case, the model finds patterns within the data itself without guidance. One well-known application is Clustering, where the model groups data points based on similarities—like clustering customers by purchasing habits.
For this project, though, we’re focused on Supervised Learning, particularly on classification tasks.
Neural Networks: a simple introduction.
When it comes to solving classification tasks using Supervised Learning, one of the most powerful models we can use is a Neural Network. Neural networks are particularly effective for tasks like image recognition, where simple models might struggle to find patterns in complex data.
But what exactly is a neural network, and why did I choose it for this project?
A toy example
Imagine you're trying to predict whether a person will go to the beach. To solve this prediction task, we'll use the simplest neural network one can build—a Perceptron. A perceptron consists of a single neuron, which is similar to a biological neuron.
We'll make our prediction based on three variables (or features): the weather, the day of the week, and availability of friends. Each of these features will be connected to the output neuron, which makes the final prediction.
As I mentioned earlier, everything is governed by math. So we can't just input to the neuron the actual values of the features, but rather a number that represents them. To achieve this, we encode the inputs and outputs as follows:
| Feature | Encoded Value |
|---|---|
| Weather | 1 if it's sunny, -1 if it's raining |
| Day of the Week | 1 if it's a weekend, -1 if it's a weekday |
| Availability of Friends | 1 if we have a friend to go with, -1 otherwise |
| Output | 1 if going to the beach, 0 otherwise |
The perceptron will combine the inputs using weights and a bias, and based on the weighted sum of these values, it will "activate" (output = 1) if the threshold is met. You can think of the weights as the importance of each connection and the bias as the predisposition of the perceptron to activate.
In the interactive section below, you can adjust the inputs, weights, and bias to see how the perceptron behaves. Try different values and see when the perceptron activates or not.
Inputs / Features
Weights / Bias
Perceptron Output:
0: Not going to the beachThis is the math that the perceptron is doing to calculate whether it will activate or not (it's updating live):
Let's break down what each term means:
- output is the result after applying the threshold: 1 if z >= 0, otherwise 0.
- z is the weighted sum of inputs plus the bias.
- x1 is the weather input.
- x2 is the day of the week input.
- x3 is the friends availability input.
- w1 is the weight of the weather input.
- w2 is the weight of the day of the week input.
- w3 is the weight of the friends availability input.
- b is the bias of the perceptron.
What all of this means is that the perceptron is taking into account not only the value of each input (weather, day and friends) but the weight each of them has and its own bias in order to "decide" to trigger.
As you experiment with different input values and weights, you’ll notice how the perceptron’s output changes.
For example, if the weight for weekday is set very high, its influence on the weighted sum is significant, which might prevent or induce the perceptron to activate, regardless of the other inputs.
Try adjusting the weight of the weekday down and see how it affects the perceptron’s activation. Similarly, you can explore how changes in the input features impact the perceptron’s output. This demonstrates how even a single perceptron can exhibit complex behavior, and hints at the possibilities when working with larger networks of neurons and multiple input features.
How does the learning happen?
If you've played around with the weights and bias in the perceptron example, you might have noticed that for each configuration of inputs, weights and bias, the perceptron behaves differently. The goal of training a model is to find the best configuration of weights and bias that makes the model predict the correct output for all the inputs in the dataset.
The weights and biases are the model. They are the parameters that can adjust and give the model its behaviour. More parameters in a model means a bigger model, often capable of more complex tasks and also more expensive to train and run. For our toy example, the number of parameters in our model is just 4: 3 weights and 1 bias. For comparison, my digits classifier model has about 100,000 parameters, and a Large Language Model (LLM) like the one behind ChatGPT has billions of parameters.
In the perceptron example, you could manually adjust the weights and bias to find the right configuration. But in a real-world scenario, you can't do this manually. Instead, you use an algorithm called Gradient Descent to automatically adjust the weights and bias based on the errors the model makes.
To start the training process we first set the weights and bias to random values (there are actually better ways to initialize these but the idea is the same). With these random values set, we feed the inputs - images of digits in our case - to the model and compare the output with the expected output. The image could be a 4 and the model predicts a 9, so -with the help of some calculus- we adjust the weights and bias so that the model would have been more likely to predict a 4, for this same input.
You can think of this process as a teacher correcting a student's mistakes. It's a repetitive process where the model makes a prediction, the error is calculated - remember that the model doesn't simply output a single prediction but rather a distribution across all of the digits so we can calculate how far off the model was from the right answer - and the weights and bias are slightly adjusted to reduce the error.
My implementation
For this project, I used a more complex neural network called a Deep Neural Network (DNN). A DNN consists of multiple layers of neurons (similar to our perceptron), each layer connected to the next. The first layer is the input layer, the last layer is the output layer, and the layers in between are called hidden layers.
In our perceptron example, we had three inputs and one output. For my implementation of the digit classifier, I used 784 input neurons (needed for the 28x28 pixel images), 128 neurons in the first hidden layer, 64 in the second hidden layer and 10 output neurons (one for each digit).
I won't bore you with much more details but you can find the full code here. The implementation is (almost) full vanilla JavaScript, using just the mathJS library for matrix operations.
The MNIST Dataset
To start training the model, I used the MNIST dataset, which contains over 100,000 samples of handwritten digits with their corresponding labels. Thanks to this publicly available dataset, I didn’t need to collect all of the data myself.
Here’s what the MNIST images look like—they are 28x28 pixels in size and grayscale.
These small, low-resolution images contain limited detail, which might seem like a disadvantage. However, less information means the model requires less computational power to train and run. And since this model needs to be able to train on my local machine and run on the browser, it can't be too expensive to run.
Canvas Drawing and Conversion
I implemented a drawing canvas on the webpage where users can draw a digit. The digit is then converted into a 28x28 grayscale image so that it matches the format of the MNIST dataset.
But even after conversion, subtle (and not so subtle) differences are clear between the MNIST images and the ones generated in my web canvas. For comparison, here’s an example of two MNIST digits (left) and two user-drawn digits after conversion (right):
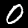
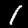
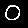
As you can tell, there is a clear difference between the stroke, shape, size or even location of the digits. This is why I needed to collect this "web generated" samples to fine-tune the model.
The initial accuracy of the model wasn’t great when tested with user-drawn digits. This phenomenon is common in machine learning and is known as distributional shift. Essentially, the images the model was trained on differ from the images it’s now being tested on. This leads to the model confidently making wrong predictions.
This distributional shift phenomenon is a common challenge in machine learning, where our training data does not match the real-world data. A simple and extreme example is image a ML model trained to drive a car in a desert, but when tested in a snowy environment, it fails to recognize the road differences and crashes.
Distributional shift can happen even when the developers are careful and collect representative data. This is because sometimes the real-world data is just too diverse and unpredictable or it even changes through time. This is why model monitoring is very important even when initial tests and performance are good.
Custom Dataset and Fine-Tuning
To improve the accuracy with user-drawn digits and compensate for the distributional shift, I created a custom dataset from user inputs. Special thanks to my friends who drew digits for 30 minutes without really understanding the purpose of it.
I then fine-tuned the model, which improved the results by reducing the "distributional shift" between the training data and the new test data.
The custom dataset contained 1,000 user-drawn digits, each labeled with the correct value. This dataset was then combined with the MNIST dataset to train the model further.
The biggest test for this step happened when you tried the demo (hopefully, the model got it right).
Conclusion
I hope this project gives you some insight into the intuition behind how these models work and are trained. As these systems become more prevalent in our daily lives, it’s important to understand the basics of how they function and the possible biases, errors, and limitations they might have.
The model I built is a simple one, but it demonstrates the core concepts of machine learning and neural networks. If you’re interested in learning more, I recommend diving into the world of machine learning and experimenting with different models and datasets.
If you've made it this far you're either my mom while I watch over your back or you're really interested in this stuff. In any case, I appreciate your time and I hope you enjoyed this project.